Piecewise exponential cumulative distribution function

ppwe computes the cumulative distribution function (CDF) or survival rate for a piecewise exponential distribution.

Usage

ppwe(
  x = 0:20,
  failRates = tibble::tibble(duration = c(3, 100), rate = log(2)/c(9, 18)),
  lower.tail = FALSE
)

Arguments

x

times at which distribution is to be computed.

failRates

Piecewise constant failure rates in rate, duration for each piecewise constant failure rate period.

lower.tail

Indicator of whether lower (TRUE) or upper tail (FALSE; default) of CDF is to be computed.

Value

A vector with cumulative distribution function or survival values

Details

Suppose \(\lambda_i\) is the failure rate in the interval \((t_{i-1},t_i], i=1,2,\ldots,M\) where \(0=t_0<t_i\ldots,t_M=\infty\). The cumulative hazard function at an arbitrary time \(t>0\) is then:

$$\Lambda(t)=\sum_{i=1}^M \delta(t\le t_i)(\min(t,t_i)-t_{i-1})\lambda_i.$$ The survival at time \(t\) is then $$S(t)=\exp(-\Lambda(t)).$$

Specification

The contents of this section are shown in PDF user manual only.

Examples

# Example: default
ppwe(seq(0:10))
#>  [1] 0.9258747 0.8572440 0.7937005 0.7637176 0.7348672 0.7071068 0.6803950
#>  [8] 0.6546923 0.6299605 0.6061630 0.5832645
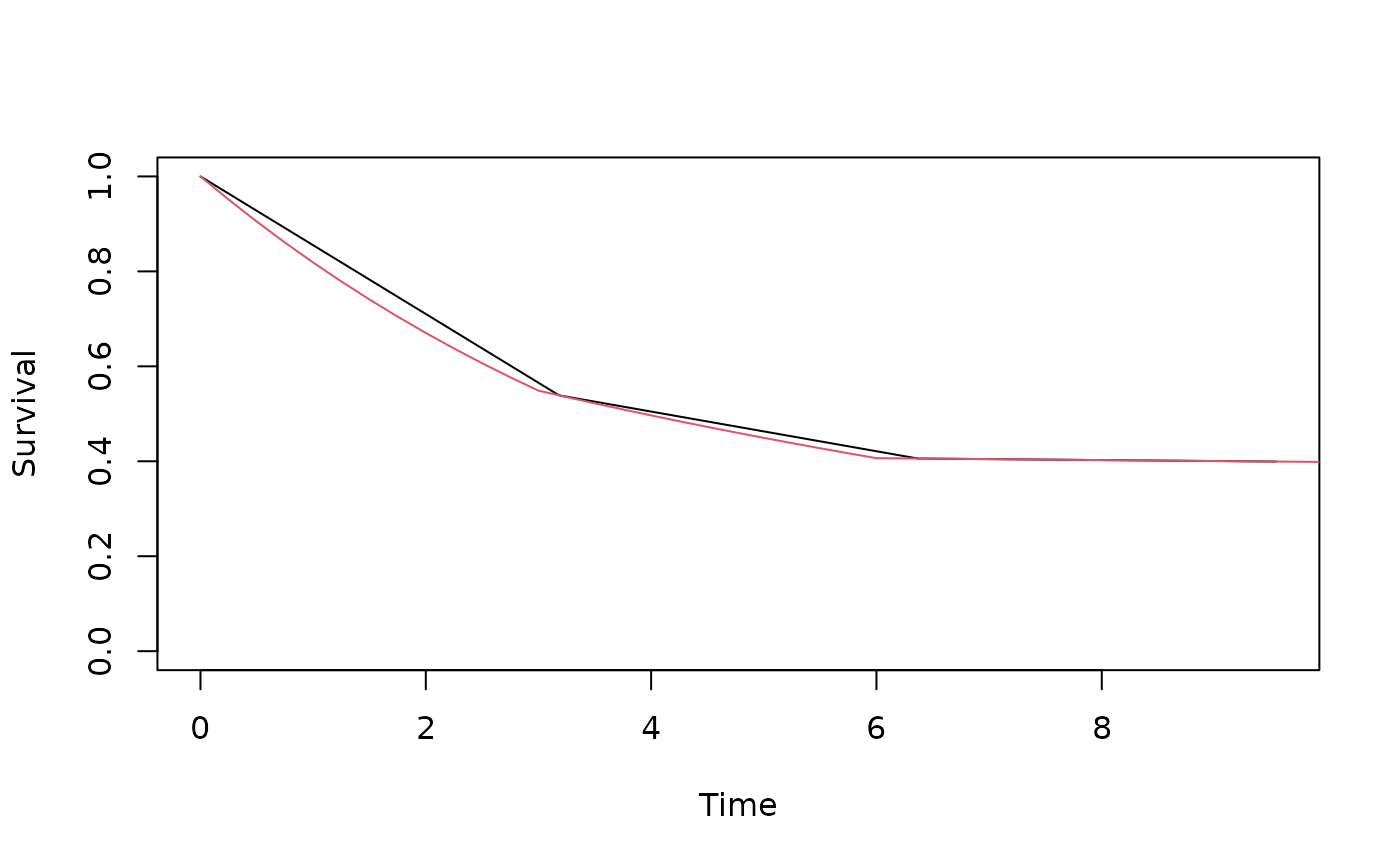
# Example: plot a survival function with 2 different sets of time values
# to demonstrate plot precision corresponding to input parameters.
fr <- tibble::tibble(duration=c(3,3,1),rate=c(.2,.1,.005))
Time <- seq(0,10,10/pi)
Survival <-  ppwe(Time,fr)
plot(Time,Survival,type="l",ylim=c(0,1))
Time <- seq(0,10,.25)
Survival <-  ppwe(Time,fr)
lines(Time,Survival,col=2)